设λ1=6，λ2=λ3=3为三阶实对称矩阵A的特征值，属于λ2=λ3=3的特征向量为，，则属于λ1=6的特征向量是（）。
考试：
科目：（在线考试）
问题：
A：
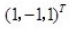
B：
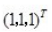
C：
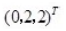
D：
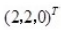
答案：
解析：
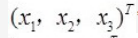(-1,0,1)，(x1,x2x3) =0，(1,2,1)，(x1,x2,x3) =0，解得x2=-x3，x1=x3;令x3=1，解得
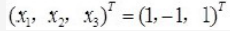。相关标签：
热门排序
推荐文章
设总体X~N(0,σ2)，X1，X2，...Xn是自总体的样本，则σ2的矩估计是:
两重物的质量均为m，分别系在两软绳上。此两绳又分别绕在半径各为r与2r并固结在一起的两圆轮上。两圆轮构成之鼓轮的质量亦为m,对轴0的回转半径为。两重物一个铅垂悬挂，一个置于光滑平面上。当系统在左重物重
水力最优断面是指当渠道的过流断面面积A、粗糙系数n和渠道底坡i一定时，其：（）。
题目请看图片
题目请看图片
质量为m的小物块在匀速转动的圆桌上，与转轴的距离为r，如图所示，设物块与圆桌之间的摩擦系数为μ，为使物块与桌面之间不产生相对滑动，则物块的最大速度为（）。
如图所示，u=（24sinωt）V，i=（4sinωt）A，ω=2000rad/s，则无源二端网络可以看作电阻R与电感L相串联，R与L的大小分别为（）。
图示矩形截面细长（大柔度）压杆，弹性模量为E。该压杆的临界载荷Fcr为：（）。
74LS161的功能见下表，如下图示电路的分频比（即Y与CP的频率之比）为（）。
JK触发器外部连接如图所示，则其输出可表达为（）。
