设函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是

设函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是
A：若{xn}收敛，则{f(xn)}收敛
B：若{xn}单调，则{f(nx)}收敛
C：若{f(xn)}收敛，则{xn}收敛
D：若{f(xn)}单调，则{xn}收敛
B
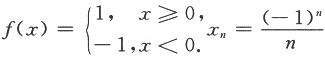(方法一)由于{xn}单调，f(xn)单调有界，则数列{f(xn)}单调有界.由单调有界准则知数列{f(xn)}收敛，故应选(B).　　(方法二)排除法：若取，则显然f(xn)单调，{xn}收敛，但显然{f(xn)}不收敛，这样就排除了(A).若取f(xn)=arctanx，x=n，则f(xn)=arctann，显然{f(xn)}收敛且单调，但{xn}不收敛，这样就排除了(C)和(D)，故应选(B).
其他工学类(电网)     数列     工学     电网     命题     单调