设L是椭圆的上半椭圆周，沿顺时针方向，则曲线积分等于（）。
考试：
科目：（在线考试）
问题：
A：
B：
C：
D：
答案：
解析：
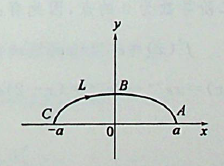如解图所示，上半椭圆ABC是由参数方程
画出的。本题积分路径L为沿上半椭圆顺时针方向，从C到B，再到A，θ变化范围由π变化到0，具体计算可由方程x=acosθ得到，起点为C（-a，0），把-a代入方程中的x，得θ=π。终点为A(a，0)，把a代入方程中的x，得θ=0，因此参数θ的变化为从θ=π变化到θ=0，即θ：π→0。由：x=acosθ可知，dx= -asinθdθ，因此原式有：
相关标签：
热门排序
推荐文章
有一玻璃劈尖，置于空气中，劈尖角为θ，用波长为λ的单色光垂直照射时，测得相邻明纹间距为l，若玻璃的折射率为n，则θ、λ、l与n之间的关系为：
如图所示，正弦电流电路中，，C=1000μF，M=6H，R=15Ω，电源的角频率ω=10rad/s，则为（）。
均质圆柱体重P，直径为D圆柱体的质量为m，半径为r，置于两光滑的斜面上。设有图示方向力F作用，当圆柱不移动时，接触面2处的约束力大小为（）。
一空调机组承担某建筑物特定区域的空气温、湿度调节，图15-3为其监控系统图。 按照图15-3中要求，AO点数为（ ）。
两台相同变压器在额定功率额定电压下并联运行,其总有功损耗为（）。
题目请看图片
题目请看图片
题目请看图片
在427问中计算得变压器的输入功率为683kW，输出功率为676kW，该变压器在此运行状态下的效率是百分之多少？( )
质量为m，半径为R的均质圆盘，绕垂直于图面的水平轴O转动，其角速度为。在图示瞬时，角加速度为O，盘心C在其最低位置，此时将圆盘的惯性力系向O点简化，其惯性力主矢和惯性力主矩的大小分别为：（）。
