设L是椭圆(a>0,b>0)的上半椭圆周,沿顺时针方向,则曲线积分等于:
考试:
科目:(在线考试)
问题:
A:
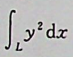
B:
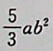
C:
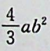
D:
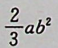
答案:
解析:
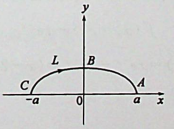 如解图所示,上半椭圆ABC是由参数方程
如解图所示,上半椭圆ABC是由参数方程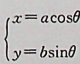 (a>0;b>0)画出的。本题积分路径L为沿上半椭圆顺时针方向,从C到B,再到A,θ变化范围由π变化到0, 具体计算可由方程x=aCOSθ沒得到。起点为C(一a,0),把-a代入方程中的x,得θ=π。终点为A(a,0),把a代入方程中的x,得 θ=0,因此参数θ的变化为从θ=π变 化到θ=0,即θ:丌→0。由x=acosθ可知,dx = — asinθdθ因此原式有:
(a>0;b>0)画出的。本题积分路径L为沿上半椭圆顺时针方向,从C到B,再到A,θ变化范围由π变化到0, 具体计算可由方程x=aCOSθ沒得到。起点为C(一a,0),把-a代入方程中的x,得θ=π。终点为A(a,0),把a代入方程中的x,得 θ=0,因此参数θ的变化为从θ=π变 化到θ=0,即θ:丌→0。由x=acosθ可知,dx = — asinθdθ因此原式有: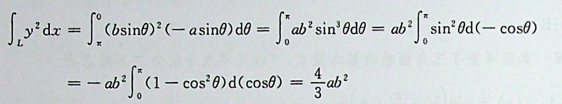
注:对坐标的曲线积分应注意积分路线的方向,然后写出积分变量的上下限,本题若取逆时针为绕行方向,则θ的范围应从θ到π。简单作图即可观察和验证。






