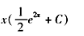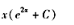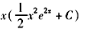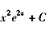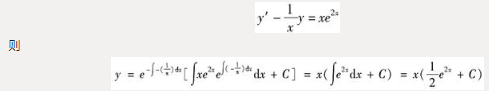微分方程的通解y等于( )。
热门排序
推荐文章
盛有浓度为0.02、体积为25的 溶液之烧杯中,滴加了浓度为0.01、体积为25的NACI容液,制得了AgCI容胶。若令该溶胶聚沉,则在同样量浓度的NaCl、、、的溶液中,聚沉能力最大的为( )溶液。
图示质量为m、长为的均质杆0A绕O轴在铅垂平面内作定轴转动。已知某瞬时杆的角速度为则杆惯性力系合力的大小为( )。
均质杆AB长为l,重W,受到如图所示的约束,绳索ED处于铅垂位置,A、B两处为光滑接触,杆的倾角为,又CD=l/4。则A、B两处对杆作用的约束力关系为( )。
在图示机构中,以角速度匀速转动,则CD杆上任意点M的速度及加速度大小为( )。
设则依次为( )。
悬臂梁AB由三根相同的矩形截面直杆胶合而成,材料的许可应力为,若胶合而开裂,假设开裂后三根杆的挠曲线相同,接触面之间无摩擦力。则开裂后的梁承载能力是原来的( )。
如图4-3-21所示,质量为m,半径为r的定滑轮O上绕有细绳。依靠摩擦使绳在轮上不打滑,并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾角为α,0<α<π/2,假设定滑轮O的轴承光
梁上无集中力偶作用,剪力图如图5-5-17所示,则梁上的最大弯矩为( )。
设,则dz等于()。
如图所示,两重物,二重物系在不计重量的软绳上,绳绕过均质定滑轮,滑轮半径为r,质量为M,则此滑轮系统的动量矩为( )。