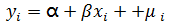假定标的物为不支付红利的股票,其现在价值为50美元,股票价格可能上涨的幅度为25%,可能下跌的幅度为20%,看涨期权的行权价格为50美元,无风险利率为7%。根据一阶段二叉树模型可推导出期权的价格为(
考试:
科目:(在线考试)
问题:
A:6.54美元
B:6.78美元
C:7.01美元
D:8.0美元
答案:
解析:
u=1+25%=1.25;d=1-20%=0.8,r=7%=0.07
股票的价格可上升至Su=50*1.25=62.5(美元);
股票价格可下跌至Sd=50*0.8=40(美元)
一阶段后期权的价值为:C(+)=MAX
C(-)=MAX
π=(1+r-d)/(u-d)=(1+0.07-0.8)/(1.25-0.8)=0.6
因此,期权价格为:C=[0.6*12.5+(1-0.6)*0]/(1+0.07)=7.01(美元)。
相关标签:
热门排序
推荐文章
最高价和最低价之间为一条竖线段,开盘价以位于竖线左侧的短横线表示,收盘价以位于竖线右侧的短横线表示的图示方法是( )。
一元线性回归模型中,为残差值,是不由和之间的线性关系所解释的变异部分。( )
在线性回归模型中,可决系数的取值范围是()。
某投资者预计9月份大豆价格将上升,利用金字塔式建仓,持续买入几次的持仓数及买入价格如下表所示。则下列空白处的持仓数可能为()。
某套利者认为豆油市场近期需求不足导致不同月份期货合约出现不合理价差,打算利用豆油期货进行熊市套利。交易情况如下表所示,则该套利者的盈亏状况为()。(交易单位:10吨/手)
如果方差膨胀因子=10,则说明第j个解释变量xj与其余解释变量之间存在严重的()问题。
某投资者预计10月份玉米价格将上升,利用金字塔式建仓,持续买入,几次的持仓数及买入价格如下表所示。则下列空白处的买入价格应分别为()。(至上而下)
某程序化交易模型在5个交易日内三天赚两天赔,一共取得的有效收益率是0.1%,则该模型的年化收益率是( )。
某投资机构持有俄罗斯政府发行的国债,该国债尚有3年剩余期限。该投资机构担心俄罗斯政府由于国内经济衰退而无法筹集足够的资金来还债并违约,所以希望在国际市场上购买CDS来规避信用风险。美国的一家投资银行为
3月12日,某套利者认为大连商品交易所7月和9月的大豆期货合约价差小于正常水平,于是进行熊市套利策略。5月15日平仓时,7月份大豆期货合约和9月份大豆期货合约的价格如下表所示,5月15日平仓时,套利者